地球化學異常的識別與提取一直是地球化學勘探的主要目標(Reimann et al ., 2005 ;Grunsky ,2007).計算機技術尤其是GIS 技術在化探界的普及, 給區域化探異常數據處理、解釋與制圖帶來了勃勃生機(Grunsky , 2007).我國實施以水系沉積物為采樣對象的全國區域化探掃面計劃近30 年, 積累了豐富的高質量的區域化探掃面數據, 這些數據為近年來大量新礦床的發現提供了有益線索.近幾年, 同行學者致力于資料的二次開發, 問題的焦點又回到了背景和異常識別上, 特別是弱緩異常的識別問題.

 

  勘查地球化學數據具有極其復雜的不規則性, 蘊含著地球化學場的豐富信息, 如:空間結構性(各向異性)、尺度不變性等特征(鮑征宇等, 1999 ;Cheng ,1999a).在地質情況復雜的區域內, 采用統一的異常下限值圈定異常的不合理性已經成為勘查地球化學家的共識, 并提出了一些確定異常下限的新方法, 主要有異常襯度法、趨勢面法、子區中位數襯度濾波法(史長義等, 1999)、空間最優U 統計量法(Cheng etal ., 1996 ;Cheng , 1999a)等.近些年來, 一些學者還探索用分形方法確定地球化學背景及異常(Cheng et al ., 1994 , 2000 ;Li et al ., 2003 ;韓東昱等, 2004), 其中局部奇異性分析方法是一種日益受到國際關注的新模型(Cheng , 1999b , 2006a ,2006b ;Chen et al ., 2007 ;Cheng and Ag terberg ,2008), 它用于指示異常的指標來自模型的冪指數α, 稱為奇異性指數, 記Δα=E -α, 這里E 表示空間維數(對二維地球化學圖E =2), 于是, Δα越大于0(即α越小于2), 則指示(正)異常強度越大.α和Δα是由局部鄰域上的多尺度計算而來, 可用來刻畫物質(或能量)的相對富集或虧損(成秋明, 2008).應用不同的化探數據處理模型, 可以得到不同的異常指示變量.這些變量可能服從不同的分布, 還可能具有不同的量綱, 如何對比這些異常指示變量對圈定異常效果的優劣?

 

  人們最為熟知的異常下限確定方法是由背景平均值加兩(或三)倍標準方差來確定, 從另一角度來看, 這種方法可視為對數據進行了標準化變換, 得到一個無量綱的標準得分(記為k), k 越大于0 , 則(正)異常強度越大.異常襯度(記為CV)是指某一元素所形成的異常含量平均值與異常所在區域的背景平均值的比值, 它作為異常清晰度的量度而廣泛使用.CV 越大于1 , 則(正)異常強度越大.元素的含量值、CV 值、Δα值等異常指示變量, 由于它們的物理意義不同、統計分布特征不同, 難以直接比較.筆者注意到, 除元素的含量值、CV 值、Δα值自身之外,還有一個與分布特征無關的量, 這就是它們的樣本排序值.樣品觀測值經某些數學變換, 如:標準化變換、正規化變換、平方根變換、對數變換后, 可以改變分布的類型、分布的形態, 有助于增強異常, 但是其共同特點之一是這些變換不改變樣品的相對排序.

 

  異常襯度法、趨勢面法等異常識別模型, 則會改變樣品排序.對同一個采樣樣品來說, 按不同的異常指示變量進行排序, 它所處的序次可能相對穩定、也可能發生較大變化, 這可在一定程度上體現出不同方法異常識別效果的趨同性或差異性.

 

  當化探取樣范圍覆蓋全區且每個取樣數據所代表的空間范圍相同時(對非規則采樣, 可經空間插值實現), 由樣品的有序排列可容易換算為空間范圍,例如排序前2 .5 %的有序樣品與研究區2 .5 %的面積是相當的.對不同異常指示變量進行排序后, 無論是對逐個樣品的比較, 還是對某一組有序樣品的比較, 它們都可視為在等面積意義下的比較.在尚未有礦產發現、研究程度較低的地區開展化探異常識別工作, 利用樣本排序方法可以簡便地確定最有潛力的地區, 如用排序取值前2 .5 %的樣品來圈定研究區2 .5 %的范圍, 并通過與地質構造背景分析來比較不同方法之間異常識別效果的異同.在已有較多礦產發現的地區, 還可借助證據權重法模型(A gterberg, 1989 ;Ag terberg et al ., 1993 ;Bonham-Carter , 1994), 通過化探異常所圈定的空間范圍與其所覆蓋或遺漏礦產兩者之間的空間相關關系來評價異常識別效果, 采用樣本排序值可克服分類標準不統一的困難, 使不同模型的異常識別結果都轉化成為等累積面積下的比較.

 

  因此, 本文擬利用順序統計量思想, 選取元素含量、異常襯度、奇異性指數作為3 種代表性的異常指示變量, 先將其轉換成對樣品的排序序次, 再按排序值來進行異常識別效果的比較.不同異常指示變量的樣本排序, 在高背景區、低背景區和有礦產出現位置處樣品各自有何特點? 用不同的異常識別模型來圈定相等的異常面積(例如占研究區2 .5 %面積),它們所確定的那些樣品各自在空間上是如何分布的? 與礦產分布的空間相關性如何? 本文將分別用排序值的X-Y plo t 圖和基于證據權法的學生t 統計量進行比較分析.CV 和Δα圈定異常的更多異同之處(包括計算方法原理、多尺度識別效果等), 限于篇幅另文闡述.

 

  1  樣本排序方法

 

  順序統計量在數學上通常是指樣本值由小到大排序而得到的統計量, 它有著廣泛的應用, 有些性質不依賴于母體分布并且計算量很小, 使用起來比較方便.本文所指的樣本排序方法約定為:按變量指示異常性能從優到劣進行排序.以樣品數為n 的元素含量Z 的一組觀測值(z1 , z2 , …, zn)為例, 按觀測值從大到小排序z1 ≥z2 ≥ … ≥z n , 記排序序列R AN K(Z)=(1 , 2 , 3 , …, n), 最佳異常樣本的排序取值rank =1 , 最差異常樣本的rank =n (大寫R AN K 表示變量, 小寫rank 表示排序取值).若其中有兩個樣品的取值相同, 按上述約定其先后順序是任意的.為了避免對R ANK(Z)取值分類時, 相同的觀測值z 處于不同的分級中, 進一步約定:將那些重復的觀測值所對應的多個有序排序值(ranks ,ranks +1 , … , rankt -1 , rankt)(n ≥t >s ≥1), 計算其排序的中位數并取整作為這一組相同觀測值共同的rank 值, 計算公式為rank =「(ranks +rank t)/2」(「」為取整符號).對CV 和Δα同樣是按降序排序得到對應的順序值R ANK (CV)和R ANK (Δα), 若對奇異性指數α, 則需按升序確定.由于受樣品分析精度的限制, 元素含量值相等的樣品可能占有一定比例, 而CV 、Δα則一般無重復值出現.

 

  本文在異常識別效果對比中采用的是樣本的排序序次(也即樣本統計量的下標索引), 而沒有用分位數.對異常指示變量按其分位數進行地球化學制圖時, 盡管分類更加直接, 但在不同方法的對比中則相對繁瑣.分位數與異常指示變量具有相同的量綱,分位數q(u)通常是按變量從小到大排序計算, 且一般約定0 <u <1 , 對CV 和Δα來說, 需換算成上側分位數q(1 -u)才對應于高異常樣品, 分位數很少用來與樣本觀測值建立一一對應關系.分位數作為一種統計量, 常用q(0 .5)表示中位數(Q2 ), 用q(0 .25)和q(0 .75)分別表示第1 四分位數(Q1)和第3 四分位數(Q3), 區間[ Q1 ,Q3] 包含了50 %的不受特異值影響的數據, 內四分位數極差IQR =Q3 -Q1 .排序序次盡管從某種程度上損失了一定信息,但更易于不同方法之間的對比, 它直接表明了不同方法處理所獲取的異常的相對強弱, 不受量綱和分布特征的影響, 與樣品一一對應, 上側rank 值與累積面積成正比.地球化學數據作為一種典型的空間數據, 在地理信息系統(GIS)支持下, 可通過“某變量在某樣品的rank 值※某樣品空間位置(x , y )※變量在某樣品的取值” 對應關系來獲取異常指示變量的取值, 變量取值及rank 值的組合也即等效于確定了順序統計量取值和上側分位數, 其中u =(rank -0 .5)/n(n 為樣本數)(Martinez and Mar tinez, 2005).

 

  2  數據來源和統計分布特征

 

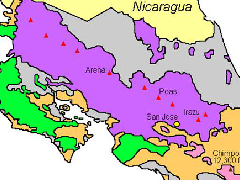
  研究區位于我國云南東南部的個舊及其周邊地區, 地理范圍為東經102°00′～ 103°30′, 北緯23°00′～ 24°00′, 面積約為18 096 km2(圖1).研究區的大地構造位置位于濱太平洋構造域與特提斯構造域交界部位, 歐亞板塊、太平洋板塊和印度板塊三者復合的碰撞擠壓帶, 屬于揚子克拉通(分區Ⅰ)、華南褶皺系(分區Ⅱ)、蘭坪-思茅褶皺系(分區Ⅲ)3 大主要構造單元的交匯部位, 其北西以師宗-彌勒深大斷裂為界(終止于紅河斷裂), 其南以紅河斷裂為界(圖1)(王寶碌等, 2004).該區在地質歷史中經歷了復雜的地質演化過程, 區內多次構造運動和強烈的巖漿活動為該區多種礦產的形成提供了有利的地質條件(莊永秋等, 1996).本區除有世界著名的以個舊錫礦為代表的滇東南錫礦帶之外, 銅礦資源也非常豐富.不同的成礦作用在不同的地質時代于不同地質構造環境中孕育了多樣化的銅礦資源.

 

  筆者系統收集了全國區域化探掃面計劃在本區的水系沉積物分析數據, 樣品數4 524 個, 按2 km ×2 km 網格密度等間距分布(58 行×78 列).EDA(ex plo rato ry data analy sis)(Tukey , 1977 ;Mar tinezand Ma rtinez , 2005)提供了優秀的描述性統計和科學數據可視化分析技術, 它的數據分析過程無需基于假設和模型.采用EDA 技術對4 524 個Cu 元素分析數據的統計分析見圖2 , 其上方圖形為直方圖和莖葉圖的疊合顯示, 下方為箱線圖, 在上側分布尾具有明顯的特異值.受測試分析精度所限, 本研究區Cu 元素含量值相等的樣品占有較大數量, 含量值為29 .8 的樣品出現頻數最多(即為眾數, 其常用對數值為1 .471 2), 達20 次, 含量取值中僅有395個數據未有重復值, 占總數的8 .73 %(圖2).按照本文約定方法, 對Cu 元素含量數據按從高到低進行排序, 得到順序值的序列記為R ANK (Raw), 稱為原始排序.圖3 展示了Cu 元素以R ANK (Raw)繪制的地球化學圖, 可見Cu 元素在分區II 具有大量高值, 相比之下, 分區Ⅰ 和Ⅱ的化探異常顯示較弱.

 

  作者按三大構造分區和地層(新生界、中生界、古生界、元古界, 巖漿巖按其侵入時代歸入對應時代的地層中)將全區化探數據分成11 類, 繪制了multiboxplo t 圖, 并將區內出現礦產位置處的樣品提取出來, 將其含量值投到對應分組的bo xplot 圖上以反映銅礦資源容礦的主要層位(圖4).由圖4 可見, 多數分組的Cu 元素含量具有特異值, 不同分組含量的集中和離散程度具有較大差異.Cu 元素極值分布最明顯、容礦數量最多的分組出現在Ⅱ-Mz(及Ⅱ-Kz)、Ⅲ-Pt 和Ⅰ-Pt , 這三大類分屬不同的構造分區,Cu 元素含量的樣本統計量(如中位數、極差、IQR等)及特異值分布均表現出明顯的差異, 銅礦產不僅出現在含量高值區, 在IQR 區間內也出現較多數量, 甚至在低于Q1 的含量區間上也占有總數的7/55 .Cu 元素的空間分布和統計特征表明, 研究區地球化學場的分布復雜, 需要挖掘空間結構、尺度特征等隱含在數據內部的深層次信息才能獲得好的異常識別效果, 弱緩異常的識別是本區化探異常找礦的關鍵.筆者以異常襯度法和局部奇異性分析法為例, 介紹它們在本地區的應用效果.

 

  3  滑動襯值和局部奇異性指數計算方法

 

  3 .1  滑動襯值

 

  異常襯度又稱襯值(cont rast value), 其計算公式為:

 

  CV(x)= za(x)/zb(x), (1)

 

  其中, za(x)為x 位置處元素在異常范圍內異常的平均值, zb(x)為x 位置處元素的背景平均值.對于網格化數據, 經常采用滑動襯值進行地球化學異常制圖, 背景值計算具體可分為常規滑動平均和逐步剔除特異值(按三倍標準方差逐步截尾)2 種方法(熊光楚等, 1997).計算窗口的選擇具有一定人為性, 本文選取的異常范圍窗口大小為1 ×1(一個單元窗口大小為2 km ×2 km , 下同), 背景窗口大小為11 ×11 .背景平均值共分4 種情形進行計算:原始數據常規滑動平均計算襯值、原始數據逐步剔除特異值計算襯值、原始數據取常用對數后的常規滑動平均計算襯值、原始數據取常用對數后的逐步剔除特異值計算襯值, 以上滑動襯值計算結果分別表示為:

 

  CV1 、CV2 、CV1(lg) 、CV2(lg).對其排序結果分別記為R ANK (CV1)、R ANK (CV2)、R ANK (CV1(lg))、R ANK(CV2(lg)).

 

  3 .2  局部奇異性分析

 

  局部奇異性度量模型可表示為(Cheng ,2006b ;陳志軍, 2007):

 

  〈z(x , l))〉=c(x)(l/L)α(x)-E , (2)

 

  其中, 〈〉表示統計期望, E 為空間維數, L 為固定的最大尺度, z(x , l))為以x 為中心在l E 空間尺度范圍上某種元素的含量, 指數α(x)表示在位置x 處的奇異性指數, 因子c(x)是在α(x)維空間中的“分形密度”(成秋明, 2008).

 

  對于網格化數據, 局部奇異性可按如下步驟計算:(a)由小到大確定滑動平均窗口:l1 ×l1 , l2 ×l2 , … , lm ×lm , 得到m 幅滑動平均圖, 記為Z1 ,Z2 , … , Zm .(b)取L =max {li }=ln , 其中i = 1 ,2 , …,m , 以lo g(Zi ×(li/ L)E)為因變量, log(li/ L)為自變量, 遍歷所有空間位置進行最小二乘擬合, 回歸直線的斜率即該位置處的α值, 令l =L , 則回歸直線擬合值即為lo g(c)值.

 

  本文選取的窗口大小序列為1 ×1 , 2 ×2 , …,11 ×11(最大窗口的范圍與計算滑動襯值時背景窗口范圍大小相等, 共6 個), L =11 進行局部奇異性指數的計算, 并轉換成Δα=E -α.分兩種情形進行計算:原始數據直接計算和原始數據取常用對數后計算, 計算結果分別表示為Δα和Δα(lg).若元素含量值有小于1 的情形, 可將含量值擴大10n 倍(可視

 

  為含量單位的變化, 如由10-6換算成10-4), 使得最小值恰能滿足大于1 , 然后再取對數進行計算.對Δα和Δα(lg)進行排序, 序次分別記為R ANK (Δα)和R ANK(Δα(lg)).

 

  3 .3  滑動襯值和局部奇異性指數的統計分布特征對不同的異常指示變量進行排序, 樣品可具有多種rank 值.對任一樣品, 也即具有以下空間位置信息和數據取值:

 

  {x , y ;z (含量值), CV1 , CV2 , CV1(lg) , CV2(lg) ,Δα, Δα(lg);R ANK (Raw), R ANK (CV1), R AN K(CV2), R ANK(CV1(lg)), R ANK (CV2(lg)), R AN K(Δα), R AN K(Δα(lg))}.

 

  圖6  Cu 元素滑動襯值和局部奇異性指數的R ANK 值色塊圖Fig .6 Geochemical mapping fo r the gliding contr ast v alues and lo cal singularity ex po nents of Cu elementa .R AN K(CV2(lg));b .R AN K(Δα);c.R A NK(Δα(lg )).各色塊圖按相同的分類標準共分12 類, 該分類標準與圖3 相同Δα計算中R 2 擬合度的樣本統計量:mean =0 .995 1 , std = 0 .009 6 , min =0 .871 7 , max =1 .000 0 ;Δα(lg)計算中R2 擬合度的樣本統計量:

 

  mean =0 .999 8 , std =0 .000 4 , min =0 .991 4 ,max =1 .000 0 .可見Δα(lg)比Δα在估值中回歸擬合優度相對更高.CV1 ,CV2 , CV1(lg) ,CV2(lg) , Δα, Δα(lg)的統計分布特征見圖5 .本文不詳細闡述CV 和Δα之間差別.實際上, CV 的大小與計算窗口大小(也即尺度)有關, 采用不同窗口大小來計算CV , 其取值可能差別很大.對Δα而言, 由于計算中采用了多尺度回歸技術, 因此理論上Δα=E -α是與尺度無關的.若α的估值具有較高的擬合度, 則α和CV 存在如下關系:α∝log(z(lm)/z(l1))log(lm/ l1) ∝lo g(CV)(擬合度R2 ※1 時), 這種近似關系可反映在圖5a 所示的X-Y plo t 圖中.當滑動襯值和局部奇異性指數的計算考慮更多因素, 例如借助空間U 統計量法在不同尺度上用各向異性的窗口(橢圓狀)代替方形窗口進行局部奇異性指數的計算, 此時的局部奇異性指數和滑動襯值就可能存在較大的差異, 異常識別的效果也將有所不同(陳志軍, 2007).在圖5a 所示的X-Y plo t 圖中, 各個橫軸變量的高值部分和低值部分相關程度均有所差異.從異常識別角度, 主要關注這些變量的高值部分.

 

  各種異常指示變量采用不同的分類標準與圖面著色方案可以制作多種形式的地球化學圖, 為便于比較, 筆者應用與R ANK(R aw)相同的分類標準和顏色渲染方案對以上滑動襯值和局部奇異性指數的排序值分別進行了地球化學制圖(圖6), R ANK(Raw ) 、R ANK (CV 1 ) 、R ANK (CV 2 )、R AN K(CV1(lg))、R ANK (CV2(lg))、R AN K (Δα)、R AN K(Δα(lg))的地球化學圖總體特征大體類似, 但在局部位置具有一定差異性.圖6 是CV1(lg) 、Δα和Δα(lg)關于rank 值分類的地球化學色塊圖, 從中可見它們均顯著降低了分區Ⅱ中的高背景, 同時還突出了分區Ⅰ和Ⅲ的異常顯示.對CV 和Δα之間異常識別效果的細節差異在排序值的地球化學圖中尚不能清晰辨別, 下面筆者就3 個方面來比較不同處理方法之間的異常識別效果.

 

  4  討論

 

  4 .1  高背景區和低背景區不同異常指示變量的排序特征筆者取R ANK (R aw)前1 .25 %的樣品(56個), 這些樣品主要分布在圖1 的分區Ⅱ , 圖7a 所示的X-Y plot 圖展示了在高背景區R ANK (Raw)、R AN K (CV1)、R ANK (CV2)、R ANK (CV1(lg))、R AN K(CV2(lg))、R AN K(Δα)和R AN K(Δα(lg))之間的異同.從圖7 中可見, 這些原始排序相對靠前的樣品, 僅有較少的樣品在CV 和Δα的樣本排序中仍然靠前, 較多樣品的排序都被下調.下調的幅度以R AN K(Δα)和R ANK(CV1)為最.這56 個高背景樣品中有部分樣品的Δα值小于0 , 從局部奇異性角度被識別為負異常.筆者由lg(Cu)的第1 四分位數1 .357 9 向低值區也取56 個樣品, 這些樣品主要分布在分區Ⅰ和Ⅲ , 從圖7b 的X-Y Plo t 圖可見, 其對原始排序的改變情形和圖7a 恰好相反, 這些原始排序相對靠后的樣品, 較多樣品的CV 和Δα的樣本排序被上調, 部分Δα值大于0 、CV 值大于1 可被篩選為異常.從圖7 可見, 滑動襯值方法和局部奇異性分析方法具有壓制高背景、突出弱緩異常的效果.

 

  4 .2  有礦位置處化探樣品不同異常指示變量的排序特征筆者采用與圖7 一樣的比較策略, 將研究區中已知礦產地位置處所對應的55 處樣品提取出來, 進而比較各類方法的排序值(圖8).從圖8a 可見, 在原始排序靠前的10 個樣品(top 3 %), 滑動襯值和局部奇異性指數的排序值略有不同, 改變幅度不大,CV 值和Δα值仍在異常可被顯著識別的區間內;而后面45 個樣品(R ANK (Raw)=100 之后), 襯值、局部奇異性指數對原始排序的改變幅度都很大.從表1 可見, 在相對低背景區, 不同異常指示變量總體上排序值升高者比降低者明顯多, 其中以Δα(lg)的rank 值升高的樣品個數最多, 約占64 %, 這使得在低背景中的某些樣品有可能被識別出來.圖8b 是按R ANK(Δα)升序排列比較, 在Δα>0 的有礦出現位置處的32 個樣品中(CV2(lg)值也都大于1), Cu 元素含量值變化范圍較大, 最高者達6 046 .3 ×10-6 ,而低者僅為33 .5 ×10-6 , 這反映襯值和局部奇異性指數對弱緩異常識別的有效性.有部分異常樣品用襯值和局部奇異性指數仍然難于識別, 這可能與水系沉積物所獲的異常與真實異常源之間具有不同程度的位移有關, 也可能由于CV 和Δα計算中需要考慮各向異性、地質構造背景的控制作用等因素, 當然還受異常下限確定方法的影響.

 

  4 .3  不同異常指示變量等面積含礦率比較與最佳異常下限確定對已有較多已知礦產發現的地區進行礦產資源定量預測工作中, 常將最大含礦率及最小漏礦率作為圈定遠景區或靶區的準則之一.這里采用證據權法來對各類異常識別模型圈定礦床(點)的效果進行比較.筆者對R ANK(Raw)、R AN K(CV1)、R ANK(CV2)、R ANK (CV1(lg))、R ANK (CV2(lg))、R ANK(Δα)和R ANK(Δα(lg))都采用相同的分類標準, 高rank 區間具有更小的分組間距, 以更精細地反映高異常區的變化性, 共分68 組不同的面積累積范圍(對于原始排序, 有些樣品具有相同R ANK 值, 約定取中位數), 從圖2 所示莖葉圖可見最多的重復出現20 次, 用rank/4 524 ×100 %來計算累積面積百分比(實際累積面積的誤差可忽略不計).在每一分類區間, 計算t 統計量, 其公式為:t =C/s(C), 其中C =W + -W - ,C 稱為對比度, 反映證據圖層同礦產的空間相關性大小,W +和W -分別稱為證據正權和證據負權, s(C)為對比度C 的標準方差.t 值越大,說明在該累積面積上化探異常與礦化關系空間相關的顯著性程度越高.從圖9 所示的累積面積-t 統計量關系圖可見, 在前50 %累積面積的那些分組中,R ANK(CV1)、R ANK(CV2)、R ANK(CV1(lg))、R AN K(CV2(lg))、R ANK(Δα)和R ANK(Δα(lg))的t曲線幾乎都在R AN K(Raw)的t 曲線上方, 也即無論按多少異常面積來進行比較, 襯值和局部奇異性指數的礦化異常識別效果將明顯優于元素含量值的效果.在1 .25 %、21 %累積面積附近, R ANK(CV 1)、R ANK (CV2)、R ANK (CV 1(lg))、R ANK（CV2(lg))、R ANK (Δα)和R AN K(Δα(lg))的t 曲線呈現上凸形狀, 而R ANK(R aw)的t 曲線則反呈下凹形狀, 在3 %累積面積附近, R ANK (Δα)和R ANK (CV 1 )的t 曲線形狀呈現為上凸而R AN K (Raw )的t 曲線則反呈下凹形狀;而在72 .5 %累積面積附近, R AN K(Raw)的t 曲線與其他的t 曲線與前50 %累積面積的凸凹情況則相反.

 

  這說明應用元素含量圈定異常, 在高背景區進行空間統計分析時, 面積的顯著增加不能保證發現礦產數量的同步增長;而在低背景處, 則可能出現較多的礦床(點), 這使得t 曲線的變化趨勢復雜多變, 很難根據R ANK(Raw)的t 曲線確定一個合適的異常范圍, 即異常下限難于確定.而對于襯度異常和局部奇異性指數來說, 其排序的t 曲線的總體變化趨勢均為:隨著累積面積的增大, t 曲線不斷向上攀升并達到頂峰(明顯高于1 .96), 然后再不斷下降.由于本研究區中成礦環境的復雜性, R ANK (CV1)、R ANK(CV2)、R ANK (CV1(lg))、R ANK(CV2(lg))、R ANK(Δα)和R ANK(Δα(lg))的t 曲線表現出一定的局部波動, 以R ANK (Δα)的t 曲線為例, 在1 .25 %、4 %、11 %、19 %、26 %累積面積處(rank =56 , 180 , 497 , 859 , 1 176)t 曲線分別達到局部極大值, 在其面積內包含的礦床(點)與發現礦產占總數比值依次為10/55 、15/55 、19/55 、26/55 和29/55 .

 

  盡管在某些位置, R ANK (CV1)、R AN K (CV2)、R ANK (CV1(lg))、R ANK (CV2(lg))的t 值略高于R ANK (Δα)和R ANK(Δα(lg)), 但總體說來,R ANK(Δα)相對更佳, 其t 曲線在前30 %面積內相對其他曲線始終保持較高的t 值.在R ANK (Δα)的t 曲線圖上確定以累積面積4 %, 11 %, 19 %作為分級閾值, 在R ANK(Δα)地球化學色塊圖上經雙線性插值生成光滑平面圖, 以rank =859(累積面積百分比19 %, Δα=0 .054)作為異常下限, 圈定了化探異常遠景區(圖10).從圖10 可見, 化探異常空間分布與多數已知礦床(點)分布的空間吻合程度較高, 在3個不同分區化探異常都有較好的顯示, 對比圖3 的高異常區基本集中分布在分區Ⅱ , R ANK (Δα)所圈定的異常圖很好地抑制了三疊系的高背景影響, 分區Ⅰ 和分區Ⅲ中一些低緩異常被較好圈定, 對未知礦床的預測提供了元素含量值所不具備的有用信息, 比用元素含量值圈定異常遠景區更具預測意義.

 

  用R ANK(CV1)、R ANK(CV2)、R ANK(CV1(lg))、R AN K(CV2(lg))和R ANK(Δα(lg))所確定的異常遠景區與R AN K(Δα)所圈定的在總體上是一致的, 這也從一個側面反映了利用Δα圈定異常的可靠性.

 

  5  結論

 

  對元素含量、滑動襯值、局部奇異性指數這些不同的異常指示變量獲取其樣本排序取值, 可以消除分布特征和量綱的影響, 在等面積條件下進行相對異常強度的比較, 對個舊及其周邊地區銅元素的水系沉積物應用結果表明, 利用樣本排序方法比較異常識別模型的效果是一種可行的方法, 這種方法可推廣應用到其他化探異常識別模型的效果對比中.

 

  異常識別模型壓制高背景、突出低緩異常的能力可從它相對樣品原始排序的優化調整情況中反映出來.在高背景區, CV 和Δα對于樣品原始排序具有顯著的降低作用;在低背景區, CV 和Δα對于樣品原始排序具有提升排序的能力.在圈定異常范圍時,CV 和Δα由于降低了高背景區樣品的排序, 避免了非礦異常面積的大量增加, 而代之以其他空間位置處弱緩異常面積的增加, 從而保持其異常范圍與礦床(點)分布具有較高程度的空間相關性, 因此,CV 和Δα這兩類方法對識別弱緩異常識別具有較好的能力.在本研究區, 通過Δα圈定了化探異常遠景區, 并被滑動襯值方法的結果所佐證, 具有較高的可信度, 在本區三個截然不同的地質構造環境分區中都確定了一定面積的異常遠景區, 比用元素含量值來圈定更具預測意義, 可為該區的銅礦資源找礦工作提供參考.局部奇異性分析方法是一種非常有效的弱緩異常識別方法.Δα可以通過原始數據直接計算, 也可取對數后計算, 在本研究區Δα通過原始數據直接計算為更佳.總體而言, 局部奇異性方法原理清晰、方法簡便、可操作性強, 在地球化學異常識別中完全可以用其替代滑動襯值方法.

 

  此外, 相對直方圖、Q-Q 圖等簡單的統計圖形,利用當今先進的計算機技術, EDA 分析技術(bo xplo t ,mat rix plo t 等)可展現更豐富的數據信息, 例如離群值分布, 在化探數據分析處理中值得廣泛推廣應用.